Irradiation on a tilted surface
In addition to direct beam and diffuse light, a tilted surface will also be struck by rays reflected off the ground.
Therefore, irradiation on a tilted surface has three components:
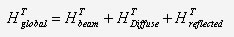
Beam Radiation
If RB denotes the ratio of the average daily beam radiation on a tilted surface to that on a horizontal surface, then the direct beam part can be written as
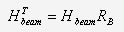
RB is a pure geometric parameter, dependent on the horizontal tilt, surface azimuth, declination angle and latitude.
Diffuse Radiation
Assuming an isotropic distribution of the diffuse radiation over the hemisphere, the diffuse part is only dependent on the horizontal tilt angle β and the diffuse radiation of the horizontal surface:

This takes into account that the tilted slope sees only a portion of the hemisphere.
Reflected Light
The energy of the reflected light is dependent on the ground’s ability to reflect, a property which is expressed by the albedo factor ρ. The albedo ranges from 0.1 (asphalt paved road) to 0.9 (snow). Given the albedo, the reflected term can be calculated from:

| |
Albedo |
| Lawn |
0.205 |
| Untilted Field |
0.26 |
| Naked Ground |
0.17 |
| Weather-beaten concrete |
0.3 |
| Asphalt |
0.15 |
| Fresh snow |
0.85 |
| Old snow |
0.58 |
The reflected light itself has parts of diffuse and parts of direct light. |
Radiation on tilted surface in relation to horizontal surface
By tilting up the panel, it may catch more light than being flat on the surface, but only up to a certain degree.
We have plotted the gains and losses in relation to a panel in the horizontal for different combinations of tilt and azimuth angles. This example applies to London at 50°Ν with an albedo of 30% on a reasonably clear day (clearness index 0.5). Under these circumstances, the optimal tilt angle would be around 40° - 16% up from the horizontal. A panel mounted on a wall (90°) would receive 18% less irradiation than a flat panel.
Intuitively, the tilting effect is more pronounced for higher latitudes
|
Optimum Surface Orientation
Tracking
In order to maximise the direct-beam insolation on a surface, it is required to rotate the surface around two axes, namely the tilt and the azimuth angle, which requires two motors. Typically, the marginal energy gains from tracing the azimuth angle are low. Hence, the second best option is to keep the slope flexible, but facing due south.
Fixed TiltIn case there is no possibility to move the surface at all, the optimal tilt angle for the maximum amount of direct beam radiation is equal to the site’s latitude. Tilting the surface up, however, causes the diffuse light portion to decrease. The optimal tilt angle for sites with humid climates is therefore 10 – 25% less than the latitude. In Germany, fFor instance, at 48°Ν, a tilt angle of 30° would be optimal, whereas in Spain, it could be up to 40°.
We have calculated the ratio of energy yield to maximum energy yield over the tilt angle for 3 different locations:
- Sri Lanka: (6°N) Near the equator, the optimal tilt angle is equal to the latitude. At 45° tilt angle, the output is reduced to 85% of the maximum.
- Lesotho: (30°S) Here, energy losses would be 10% off the maximum if module was in horizontal, but only 4% if tilted at 45°.
- Hamburg, Germany: (53°N) As mentioned above, the optimal tilt angle is close to 30°. At 45° tilt, the energy yield is stil very close to the maximum. This wide range of acceptable tilt angles makes roof installations attractive in higher latitudes.
|
|
|
Seasonal Tilt
In regions where most of the irradiance occurs in summer, it may be beneficial to adjust the tilt angle for winter and summer. In Germany, 75% of solar irradiance is experienced from April to September. The optimal angle for the summer would be 27° and for winter 50°, rather than 30° if the modules couldn't be tilted at all. In Spain, seasonal differences are less pronounced (summer accounts for 60%), making a seasonal tilt less critical. |



